
La loterie est un jeu de hasard qui attire de nombreux joueurs qui espèrent décrocher le gros lot. Et elle peut en réalité être déchiffrée à l’aide de l’analyse mathématique. Des mathématiciens de l’université de Manchester ont trouvé le nombre minimum de tickets à acheter pour garantir un gain au loto, découvrant une réponse surprenante qui remet en question les croyances populaires sur la loterie.
La quête du nombre magique de billets
Plongeant dans le jeu de loto de la loterie nationale britannique, où six numéros doivent être choisis entre 1 et 59, les chercheurs ont exploré les mystères des combinaisons gagnantes. Du simple duo de numéros à la précieuse cagnotte de six numéros identiques (culminant à 7,8 millions de livres sterling, soit 9,9 millions de dollars), le désir de gagner a suscité des questions : quel est le nombre minimum de billets nécessaires pour garantir un gain ?
La réponse n’est pas ce que l’on pourrait imaginer. Les mathématiciens David Stewart et David Cushing ont résolu l’énigme en déterminant qu’avec seulement 27 billets, il était possible d’assurer la correspondance d’au moins deux numéros parmi les 45 057 474 combinaisons potentielles.

Les plans de Fano : Concevoir la route de la victoire
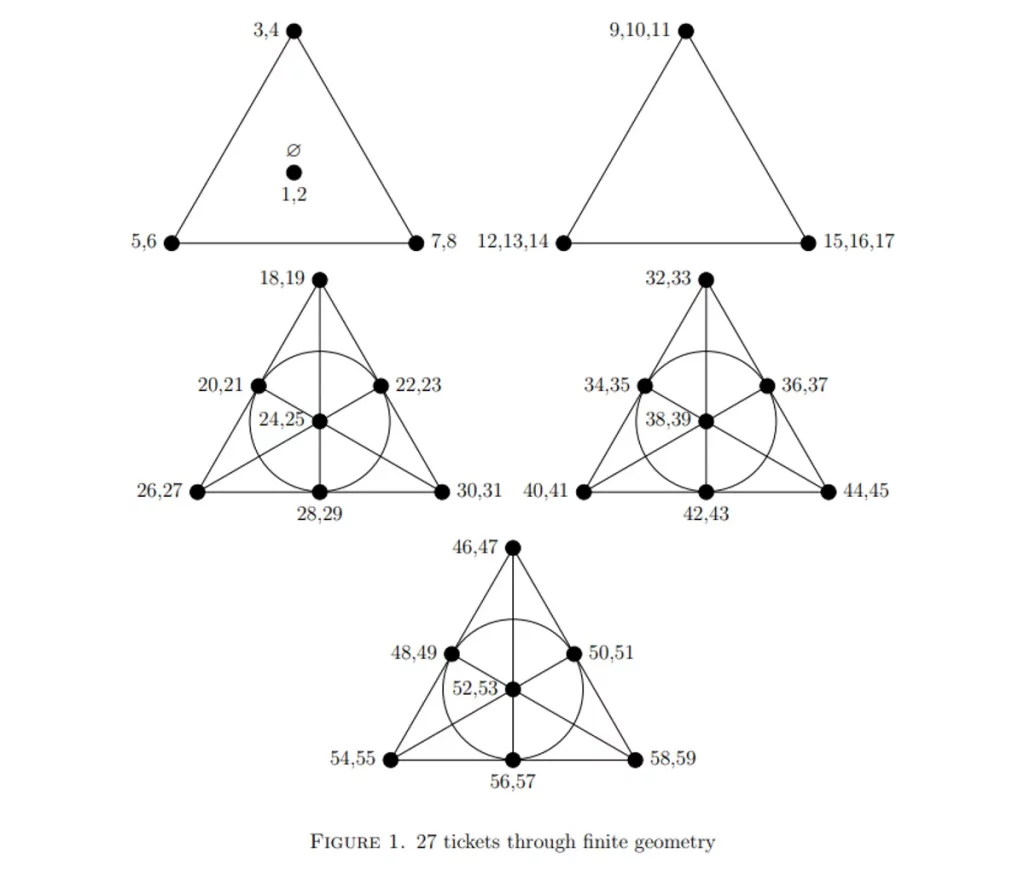
Pour décrire ces combinaisons complexes, les mathématiciens ont exploité les « plans de Fano », des structures géométriques qui transcendent la loterie en des modèles abstraits. Ces plans consistent en des triangles qui renferment des paires de nombres, unies par des lignes droites ou courbes. Chaque ligne relie trois paires, créant ainsi une multitude de configurations victorieuses potentielles.
Cependant, l’intérêt majeur ne réside pas simplement dans la victoire au loto, mais dans l’élucidation du nombre optimal de billets nécessaires pour gagner. Établir qu’il était impossible de triompher avec seulement 26 billets s’est avéré être un défi mathématique complexe, mais fascinant.
“En gros, il y a une contrainte qui vient du fait qu’il n’y a que 156 entrées sur 26 tickets. Cela signifie que beaucoup de numéros ne peuvent pas apparaître plusieurs fois. On finit par trouver six numéros qui n’apparaissent sur aucun ticket à la fois. En termes de théorie des graphes, nous finissons par prouver l’existence d’un ensemble indépendant de taille six”, a expliqué M. Stewart, maître de conférences en mathématiques pures à l’université de Manchester.
La mise en pratique : réalité vs théorie
La théorie, bien qu’intéressante, n’est que le point de départ. Peter Rowlett, un mathématicien, a souligné dans The Aperiodical que dans 99 % des cas, l’investissement en billets ne compenserait pas les gains. La victoire serait certes présente, mais les bénéfices seraient minimes. Pourtant, l’équipe de recherche a décidé de mettre la théorie en action.
Ainsi, avant le tirage du 1er juillet 2023, les chercheurs ont acquis 27 billets de loto pour une somme de 54 livres sterling (68,61 dollars). Parmi ces billets, trois se sont avérés gagnants, avec une paire de numéros correspondants sur chacun d’eux. Cela leur a permis de gagner des billets gratuits aléatoires pour les tirages suivants, cependant, aucun de ces billets n’a décroché le jackpot.
En définitive, l’approche mathématique de la loterie représente plus une curiosité intrigante qu’une véritable stratégie pour devenir riche rapidement. La recherche des mathématiciens de l’université de Manchester remet en question certaines idées préconçues sur la loterie, et bien que garantir une victoire avec 27 billets soit une réalité, il est important de se rappeler que la réalité du jeu peut varier considérablement par rapport à la théorie.
Par ailleurs, un homme a gagné 14 fois à la loterie en utilisant un principe mathématique simple.
Par Eric Rafidiarimanana, le
Source: IFL Sience
Étiquettes: mathematique, billets, loterie
Catégories: Actualités, Société
