Le problème mathématique du canapé a peut-être enfin trouvé une solution

Lorsqu’on déménage, on ne pense généralement pas aux mathématiques. Et pourtant, depuis près de 60 ans, un problème complexe a empêché de nombreux foyers d’installer des meubles dans des espaces restreints. Il s’agit d’une question géométrique vieille de plusieurs décennies : quel est le plus grand canapé capable de passer un coin étroit en L ? Jineon Baek, un chercheur passionné par la combinatoire et la géométrie de l’université Yonsei en Corée, a récemment publié une démonstration de 100 pages sur ce problème, apportant enfin une solution.

Le problème du sofa

Tout a commencé en 1966, lorsque Leo Moser, un mathématicien austro-canadien, a formulé ce problème qui semble simple à première vue : comment faire passer le plus grand objet bidimensionnel à travers un coin en forme de L ? Cela peut paraître trivial, mais la solution requiert une réflexion complexe sur la géométrie et la combinatoire. 

Lire aussi Le célèbre paradoxe de Stephen Hawking sur les trous noirs est peut-être résolu

Par exemple, une chaise carrée de petite taille passe facilement, mais un canapé rectangulaire un peu plus grand bloque instantanément le passage. Le défi était alors de déterminer la taille maximale que pouvait avoir un objet bidimensionnel capable de franchir un coin étroit.

Ce problème a trouvé ses racines dans des questions plus anciennes liées à la navigation des espaces étroits. L’un des premiers résultats dans ce domaine est celui de John Hammersley qui, en 1968, a proposé une solution en utilisant un canapé de forme étrange, un peu comme un puzzle géométrique. Ce canapé avait une superficie de 2,2074 unités et pouvait, tout juste, se glisser à travers l’angle. Hammersley a également établi une limite théorique, affirmant qu’aucun canapé ne pourrait dépasser 2,8284 unités sans rester bloqué.

Des améliorations progressives

Au fil des années, d’autres chercheurs ont affiné la solution de Hammersley. En 1992, Joseph Gerver, un professeur de l’université Rutgers, a modifié la conception du canapé en arrondissant certains bords et en ajoutant des courbes plus fines. Il a réussi à augmenter légèrement la surface du canapé, atteignant 2,2195 unités. Bien qu’il ait démontré que cette forme était optimisée dans le cadre des conditions définies, une question subsistait : cette solution était-elle la meilleure possible ?

Lire aussi Les dauphins du golfe du Mexique sont testés positifs au fentanyl

Le problème est devenu plus difficile à résoudre à mesure que les formes du canapé se diversifiaient. Mais en 2018, deux chercheurs, Yoav Kallus et Dan Romik, ont utilisé des outils informatiques pour explorer encore plus loin, atteignant la taille de 2,37 unités pour le canapé. Cela marquait un nouveau progrès dans la quête pour comprendre la géométrie de ces objets.

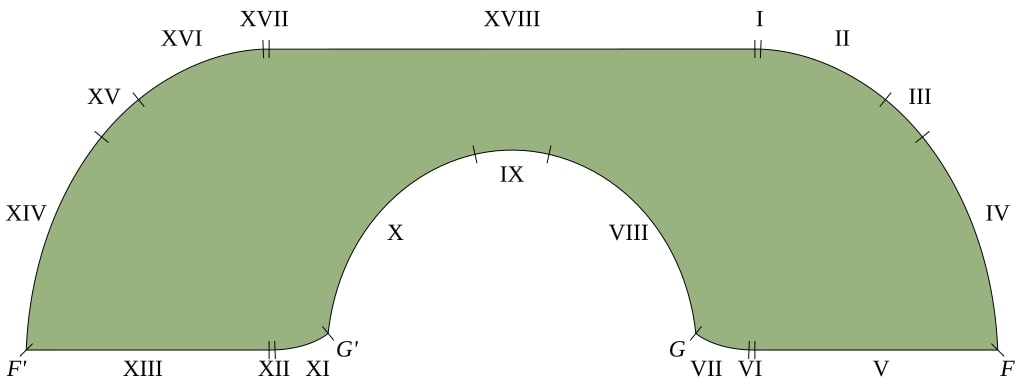
La solution finale de Jineon Baek

C’est là qu’intervient Jineon Baek, qui a réussi à prouver que la solution de Gerver, bien que déjà impressionnante, était effectivement la taille optimale du canapé dans un couloir d’une unité de largeur. Grâce à une approche mathématique avancée, Baek a utilisé des outils modernes de combinatoire pour verrouiller les propriétés de la forme optimale et étendre cette démonstration à d’autres dimensions. Il a ainsi confirmé, une fois pour toutes, que la superficie maximale d’un canapé pouvant passer un coin étroit est bien de 2,2195 unités, comme l’avait proposé Gerver en 1992.

Bien que la démonstration de Baek n’ait pas encore été examinée par ses pairs, elle pourrait clore définitivement ce débat qui a duré plusieurs décennies. Sa recherche montre non seulement une avancée dans la géométrie, mais aussi l’importance de la persévérance dans la résolution de problèmes apparemment simples, mais d’une grande complexité sous-jacente.

Lire aussi Des chercheurs créent un vaccin contre le tétanos administré sous forme de crème

Par ailleurs, la « conjecture du lit superposé » en mathématiques a été réfutée après près de 40 ans.