Pourquoi 2+2 peut parfois faire 5 sans que personne ne se trompe : le paradoxe qui trouble les mathématiques

Additionner semble simple… jusqu’à ce que le contexte brouille les cartes. Entre mélange de liquides, arrondis flous ou concepts abstraits, 2 + 2 peut ne pas faire 4, sans erreur de calcul. Un paradoxe fascinant, rarement discuté, pourtant omniprésent dans nos vies.

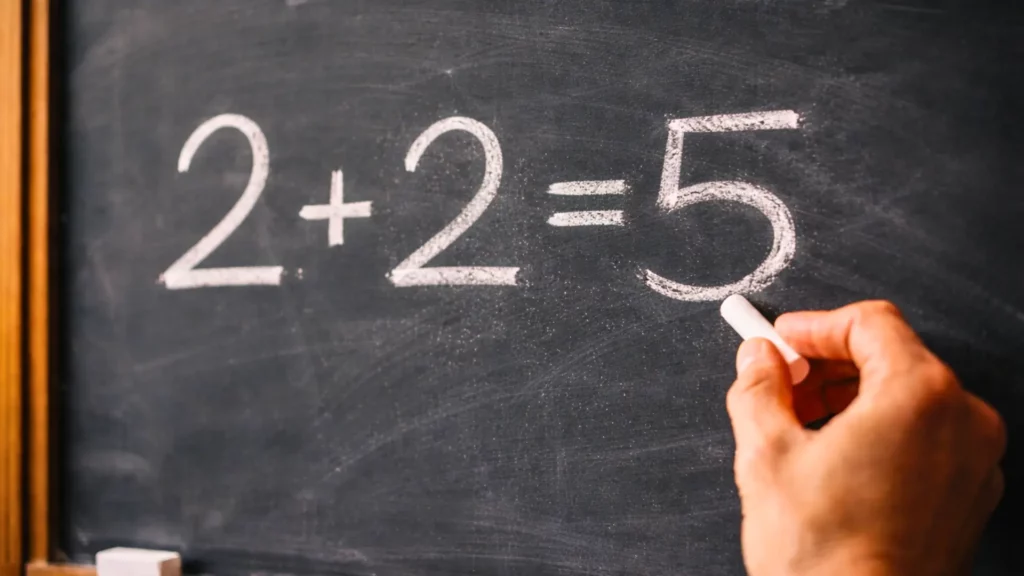
Mélanger des éléments modifie les volumes : quand la logique additive échoue dans le réel

Prenez deux verres de 200 ml d’eau. Logiquement, vous devriez obtenir 400 ml en les versant dans un même récipient. Sauf que… non. Si l’un est froid et l’autre chaud, la dilatation thermique modifie légèrement le volume total. Encore plus flagrant : essayez avec un peu d’huile et de farine. En cuisine, les volumes ne s’ajoutent pas, ils interagissent. Deux cuillères + deux cuillères ne font pas quatre, mais un mélange.

Lire aussi Montrer l’invisible : la sonde Parker de la NASA révèle de nouveaux secrets brûlants du Soleil

Ce phénomène dépasse la cuisine. En biologie, en chimie ou en physique, le monde réel n’obéit pas toujours à la logique des manuels scolaires. Les éléments combinés changent d’état, interagissent, fusionnent. Et dans ces cas-là, l’addition classique ne suffit plus à décrire ce qui se passe.

Des arrondis aux conventions : comment les règles du calcul influencent le résultat final

Imaginez que vous mesuriez deux valeurs à 2,3. Si vous arrondissez chacune à 2, vous obtenez 2 + 2 = 4. Mais si vous additionnez d’abord (2,3 + 2,3 = 4,6) et que vous arrondissez ensuite, vous obtenez 5. Même calcul, mêmes données, deux résultats différents, juste à cause d’une convention.

Ce n’est pas une triche : c’est un choix. Un choix parmi d’autres possibles. Les mathématiques fonctionnent selon des règles, mais ces règles peuvent varier selon les disciplines, les logiciels, les standards. Et dès que ces règles changent, le résultat évolue aussi. Ce n’est pas une erreur. C’est un rappel que le chiffre, parfois, n’est qu’un reflet du cadre dans lequel on l’utilise.

Lire aussi Réchauffement climatique : la Terre s’apprête à perdre 3 000 glaciers chaque année

Quand les chiffres traduisent des idées floues : le piège des mesures abstraites

Un test de QI, une évaluation de stress, une mesure d’agressivité… Tous ces chiffres semblent objectifs, mais ils sont en réalité des interprétations chiffrées de phénomènes humains. Traduire l’intelligence ou le bien-être en une note, c’est déjà un choix arbitraire, dicté par des critères souvent invisibles.

Ajouter deux scores d’agressivité ou de stress, est-ce vraiment comme additionner deux pommes ? Non. Ce que l’on additionne ici, ce ne sont pas des entités mesurables, mais des représentations floues, souvent influencées par des biais culturels, sociaux ou méthodologiques. L’illusion de précision masque une profonde instabilité.

Dans ces contextes, 2 + 2 peut faire 5, ou 3, ou rien du tout, selon la manière dont les données sont construites et interprétées. C’est pourquoi les sondages, les indices ou les baromètres doivent être lus avec prudence : les chiffres sont là, oui, mais ils ne disent pas toujours ce qu’on croit qu’ils disent.

Lire aussi Certains cerveaux seraient programmés pour devenir accros au cannabis : ce que révèle une expérience troublante sur les rats

Additionner dans un cercle ou une boucle : pourquoi certains systèmes défient les mathématiques classiques

Prenez un angle de 360°. Ajoutez-lui 360°. Vous obtenez 720°, mais… vous revenez au point de départ. Dans un cercle, certains ajouts ne produisent pas de changement visible. Même chose si vous vissez une vis cinq fois au lieu de quatre : la position finale est la même, mais l’effort fourni diffère.

Dans ces systèmes fermés, 2 + 2 peut très bien donner 0, ou 1, ou 5, selon ce que l’on observe. Ce n’est pas une erreur, c’est une propriété du système. Le calcul est juste, mais l’interprétation doit changer. C’est un bon rappel que le sens d’un résultat dépend souvent plus de ce qu’on cherche à mesurer que du chiffre lui-même.

Ce que ce paradoxe révèle sur notre rapport aux mathématiques

Ce qu’on appelle une “erreur” est souvent un défaut de cadre, pas de calcul. La force des mathématiques réside dans leur rigueur. Mais cette rigueur repose sur des hypothèses, des définitions, des contextes. Et dès qu’on sort de ces cadres, les résultats prennent une toute autre tournure.

Lire aussi Le cerveau peut fuir la réalité sur commande : la science valide ce pouvoir mental que les jeunes nomment « shifting »

Alors oui, parfois 2 + 2 peut faire 5, et non, cela ne remet pas en cause les mathématiques. Cela nous oblige simplement à penser plus finement ce que l’on compte, et pourquoi on le compte. Derrière chaque opération, il y a une intention, un contexte, une grille de lecture qu’on ne peut ignorer.