La solution à un problème mathématique extrêmement complexe vieux de 100 ans enfin trouvée

Il existe dans le domaine des mathématiques de nombreux problèmes non résolus. Parmi ces problèmes figure la conjecture de Kakeya dans un système à trois dimensions. Plus d’un siècle après la formulation initiale de ce problème, des mathématiciens semblent avoir enfin trouvé une solution pour le résoudre.

Qu’est-ce que la conjecture de Kakeya ?

Imaginez un crayon posé sur votre bureau. Essayez de le faire tourner de manière qu’il pointe dans chaque direction, mais veillez à ce qu’il effleure le moins possible la surface du bureau. Autrement dit, l’objectif est de faire tourner le crayon à 360 degrés de manière à minimiser l’espace qu’il traverse. La question est de savoir comment. Cette énigme a été formulée pour la première fois par le mathématicien japonais Sōichi Kakeya en 1917. Pour la plupart des gens, la réponse semble évidente : il suffit de faire pivoter le crayon (ou plus précisément l’aiguille d’après la formulation originale) en son centre.

Lire aussi Cap Canaveral devient le terrain de jeu privé de SpaceX : 3 sites dédiés à Starship pour viser la Lune… ou plus

Ce n’est pourtant pas la bonne réponse. Il existe en effet une autre méthode qui permet une meilleure optimisation de l’espace : faire bouger l’aiguille suivant des formes comme le deltoïde, une forme grossièrement triangulaire. Le deltoïde permet d’avoir une aire beaucoup plus petite que le cercle qui entourerait la même aiguille si elle tournait statiquement en son centre. Les ensembles de points de l’espace euclidien dans la solution mathématique de ce problème est ce que l’on appelle l’ensemble de Kakeya. En 1919, le mathématicien russe Abram Besicovitch a même montré qu’il est possible d’avoir un espace de mesure nulle.

Cependant, cette solution n’est valable que si l’aiguille est placée sur une surface plane, c’est-à-dire en deux dimensions. Qu’en est-il dans un espace tridimensionnel ? Ce second problème est la base de ce que l’on désigne par la conjecture de Kakeya. Cette conjecture stipule que le nombre de dimensions de la forme tracée correspondra toujours au nombre de dimensions de l’espace dans lequel elle se trouve. En tant que conjecture, cette formulation est cependant purement théorique, puisqu’elle n’a jamais été démontrée de manière pratique. Du moins, c’était le cas jusqu’à récemment.

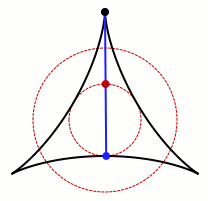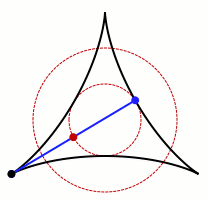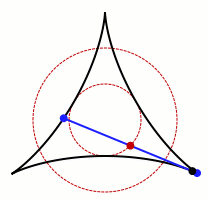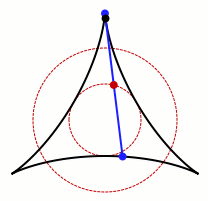
Une démonstration de la conjecture de Kakeya dans un espace en 3D

Deux chercheurs, Joshua Zahl de l’université de Colombie-Britannique au Canada et Wang Hong de l’université de New York, auraient en effet réussi à réaliser cette fameuse démonstration. Dans un article de 127 pages prépublié sur arXiv, les chercheurs décrivent comment l’aiguille peut se déplacer en trois dimensions. Il faut savoir qu’auparavant, les mathématiciens ont émis l’hypothèse selon laquelle un ensemble de Kakeya dans un espace tridimensionnel doit avoir une dimension de Hausdorff (un nombre réel positif) de 3, ce qui signifie qu’il remplit pratiquement tout l’espace.

Lire aussi Révolution énergétique : ce réacteur français détruit plus de déchets qu’il n’en produit et séduit les États-Unis

Cette étude confirme cette conjecture, démontrant que de tels ensembles ne peuvent être trop petits malgré leur capacité à contenir des lignes pointant dans toutes les directions. Les chercheurs ont également établi qu’un ensemble de Kakeya en trois dimensions a une dimension de Minkowski (une autre mesure de la dimension fractale) de 3. Notons que la résolution de ce problème est très importante, même au-delà des mathématiques et de la géométrie. En fait, ça a aussi des implications majeures dans des domaines comme l’informatique et la cryptographie.

Par ailleurs, un homme a gagné 14 fois à la loterie en utilisant un principe mathématique simple.